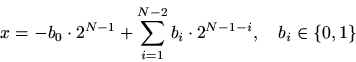NOTE: THIS DOCUMENT IS OBSOLETE, PLEASE CHECK THE NEW VERSION: "Mathematics of the Discrete Fourier Transform (DFT), with Audio Applications --- Second Edition", by Julius O. Smith III, W3K Publishing, 2007, ISBN 978-0-9745607-4-8. - Copyright © 2017-09-28 by Julius O. Smith III - Center for Computer Research in Music and Acoustics (CCRMA), Stanford University
<< Previous page TOC INDEX Next page >>
General Formula for Two's-Complement, Integer Fixed-Point Numbers
Let
denote the (even) number of bits. Then the value of a two's complement integer fixed-point number can be expressed in terms of its bits
as
We visualize the binary word containing these bits as
Each bitis of course either 0 or 1. Check that the
table above is computed correctly using this formula. As an example, the numer 3 is expressed as
while the number -3 is expressed as
and so on.The most-significant bit in the word,
, can be interpreted as the ''sign bit''. If
The least-significant bit is
. ''Turning on'' that bit adds 1 to the number, and there are no fractions allowed.
The largest positive number is when all bits are on except
. The largest (in magnitude) negative number is
, i.e.,
and
for all
. Table 4.5 shows some of the most common cases.
Table 4.5:Numerical range limits in
8 -128 127 16 -32768 32767 24 -8,388,608 8,388,607 32 -2,147,483,648 2,147,483,647
