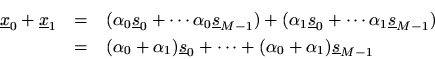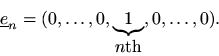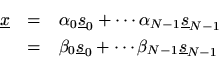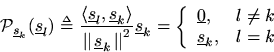This section summarizes and extends the above derivations in a
somewhat formal manner (following portions of chapter 4 of
).
Definition: A set of vectors is said to form a vector space
if given any two members 
and 
from the set, the vectors 
and 
are also in the set, where 
is any
scalar.
Vectors defined as a list of 
complex numbers
, using elementwise addition and
multiplication by complex scalars 
, form a vector space. Similarly, real vectors 
and real scalars form a vector space.
Theorem: The set of all linear combinations of any set of
vectors from 
or 
forms a vector space.
Proof: Let the original set of vectors be denoted
, where 
can be any integer greater than zero. Then any member
of the vector space is by definition a linear combination of
them:
From this we see that 
is also a linear combination of the original vectors, and hence
is in the vector space. Also, given any second vector from the
space 
, the sum is
which is just another linear combination of the original vectors,
and hence is in the vector space. It is clear here how the closure
of vector
addition and scalar multiplication are ''inherited'' from the
closure of real or complex numbers under addition and
multiplication.
Definition: If a vector space consists of the set of all
linear combinations of a finite set of vectors , then those vectors are said to span the
space.
Example: The coordinate vectors in
span
since every vector 
can be expressed as a linear combination of the
coordinate vectors as
where 
, and 
, 
, 
, and so on up to 
.
Theorem: (i) If span a vector space, and if one of them, say
, is linearly dependent on the others, then the vector
space is spanned by the set obtained by omitting from the original set. (ii) If span a vector space, we can always select from
these a linearly
independent set that spans the same space.
Proof: Any in the space can be represented as a linear
combination of the vectors . By expressing as a linear combination of the other vectors in the set,
the linear combination for becomes a linear combination of vectors other than . Thus, can be eliminated from the set, proving (i). To prove
(ii), we can define a procedure for forming the require subset of
the original vectors: First, assign 
to the set. Next, check to see if and 
are linearly dependent. If so (i.e., is a scalar times ), then discard ; otherwise assign it also to the new set. Next, check to
see if 
is linearly dependent on the vectors in the new set. If it
is (i.e., is some linear combination of and ) then discard it; otherwise assign it also to the new set.
When this procedure terminates after processing 
, the new set will contain only linearly independent
vectors which span the original space.
Definition: A set of linearly independent vectors which
spans a vector space is called a basis for that vector
space.
Definition: The set of coordinate vectors in is
called the natural basis for ,
where the 
th
basis
vectoris
Theorem: The linear combination expressing a vector in terms
of basis vectors for a vector space is unique.
Proof: Suppose a vector can be expressed in two different ways as a linear
combination of basis vectors 
:
where 
for at least one value of 
.
Subtracting the two representations gives
Since the vectors are linearly independent, it is not possible to
cancel the nonzero vector 
using some linear combination of the
other vectors in the sum. Hence, 
for all 
.
Note that while the linear combination relative to a particular
basis is unique, the choice of basis vectors is not. For example,
given any basis set in , a new basis can be formed by rotating all
vectors in by the same angle. In this way, an infinite number of basis
sets can be generated.
As we will soon show, the DFT can be viewed
as a change of coordinates from coordinates relative to the
natural basis in , 
, to coordinates relative to the sinusoidal basis
for ,
, where 
. The sinusoidal basis set for
consists of length sampled complex sinusoids
at frequencies 
. Any scaling of these vectors in
by
complex scale factors could also be chosen as the sinusoidal basis
(i.e., any nonzero amplitude
and any phase will do). However, for simplicity, we will only use
unit-amplitude, zero-phase complex sinusoids as the Fourier
''frequency-domain''
basis set. To summarize this paragraph, the time-domain samples of
a signal are its coordinates relative to the natural basis for
,
while its spectral coefficients are the coordinates of the signal
relative to the sinusoidal basis for .
Theorem: Any two bases of a vector space contain the same
number of vectors.
Proof: Left as an exercise (or see [3]).
Definition: The number of vectors in a basis for a
particular space is called the dimension of the space. If
the dimension is ,
the space is said to be an
dimensional space, or -space.
In this course, we will only consider finite-dimensional vector
spaces in any detail. However, the discrete-time Fourier transform
(DTFT) and Fourier transform both require infinite-dimensional
basis sets, because there is an infinite number of points in both
the time and frequency domains.
Theorem: The projections of any vector onto any orthogonal
basis set for can be summed to reconstruct exactly.
Proof: Let 
denote any orthogonal basis set for
.
Then since is in the space spanned by these vectors, we
have
for some (unique) scalars 
. The projection of onto 
is equal to
(using the linearity of the projection operator which follows from
linearity of the inner
product in its first argument). Since the basis vectors are
orthogonal, the projection of 
onto is zero for
:
We therefore obtain
Therefore, the sum of projections onto the vectors is just the linear combination of the which forms .
<< Previous page TOC INDEX Next
page >>
