NOTE: THIS DOCUMENT IS OBSOLETE, PLEASE CHECK THE NEW
VERSION: "Mathematics of the Discrete
Fourier Transform (DFT), with Audio Applications --- Second
Edition", by Julius
O. Smith III, W3K
Publishing, 2007, ISBN 978-0-9745607-4-8. - Copyright ©
2017-09-28 by Julius O. Smith III -
Center for Computer Research
in Music and Acoustics (CCRMA), Stanford University
<<
Previous page TOC INDEX Next
page >>
Like the 
operator, the 
operator maps a length
signal to
a length 
signal:
Definition: The repeat 
times operator is defined by
where . Thus, the operator simply repeats its input signal
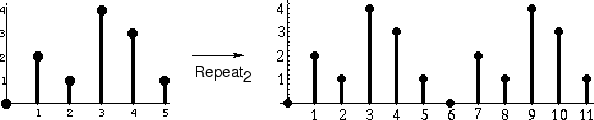
times.8.4An example of 
is shown in Fig. 8.6.
The example is
Figure:Illustration of
.
|
|
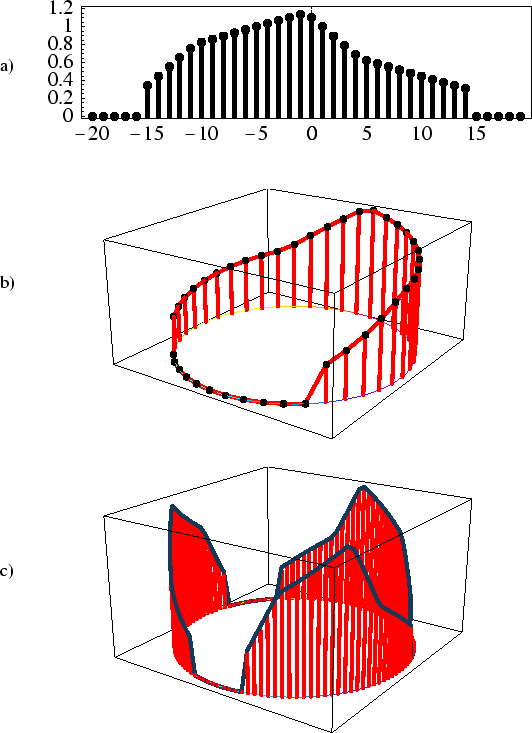
A frequency-domain
example is shown in Fig. 8.7.
Figure 8.7a
shows the original spectrum 
,
Fig. 8.7b
shows the same spectrum plotted over the unit circle in the
plane,
and Fig. 8.7c
shows 
. The 
point (dc) is on the right-rear face of the enclosing box.
Note that when viewed as centered about 
,
is a
somewhat ''triangularly shaped'' spectrum. The repeating block can
be considered to extend from the point at to the
point far to the left, or it can be considered the triangularly
shaped ''baseband'' spectrum centered about .
Figure:Illustration of
. a) Conventional plot of . b) Plot
of over the
unit circle in the plane. c) .
|
|
The repeat
operator is used to state the Fourier
theorem
That is, when you stretch a signal by the factor , its
spectrum is repeated times around the unit circle.
<<
Previous page TOC INDEX Next
page >>
