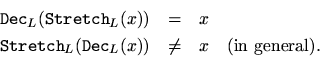NOTE: THIS DOCUMENT IS OBSOLETE, PLEASE CHECK THE NEW VERSION: "Mathematics of the Discrete Fourier Transform (DFT), with Audio Applications --- Second Edition", by Julius O. Smith III, W3K Publishing, 2007, ISBN 978-0-9745607-4-8. - Copyright © 2017-09-28 by Julius O. Smith III - Center for Computer Research in Music and Acoustics (CCRMA), Stanford University
<< Previous page TOC INDEX Next page >>
Decimation Operator
Definition: Decimation byis defined as taking every
:
The
operator maps a length
signal down to a length
signal. It is the inverse of the
operator (but not vice versa), i.e.,
The stretch and decimation operations do not commute because they are linear time-varying operators. They can be modeled using time-varying switches controlled by the sample index.
Figure:Illustration of . The white-filled circles indicate the retained samples while the black-filled circles indicate the discarded samples.
An example of
is shown in Fig. 8.8. The example is
