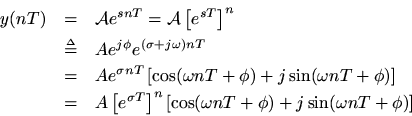NOTE: THIS DOCUMENT IS OBSOLETE, PLEASE CHECK THE NEW VERSION: "Mathematics of the Discrete Fourier Transform (DFT), with Audio Applications --- Second Edition", by Julius O. Smith III, W3K Publishing, 2007, ISBN 978-0-9745607-4-8. - Copyright © 2017-09-28 by Julius O. Smith III - Center for Computer Research in Music and Acoustics (CCRMA), Stanford University
<< Previous page TOC INDEX Next page >>
Sampled Sinusoids
In discrete-time audio processing, such as we must do on a computer, we work with samples of continuous-time signals. Let
denote thesampling rate in Hz. For audio, we typically have
kHz, since the audio band nominally extends to
kHz. For compact discs (CDs),
kHz (or very close to that--I once saw Sony device using a sampling rate of
Hz), while for digital audio tape (DAT),
kHz.
Let
denote the sampling period in seconds. Then to convert from continuous to discrete time, we replace
by
, where
is an integer interpreted as the sample number.
The sampled generalized complex sinusoid (which includes all other cases) is then