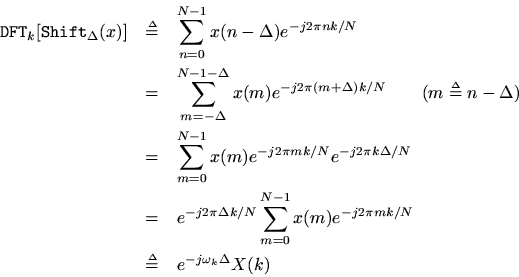Shift Theorem

GUIDE: Mathematics of the Discrete Fourier Transform (DFT) - Julius O. Smith III. Shift Theorem

NOTE: THIS DOCUMENT IS OBSOLETE, PLEASE CHECK THE NEW VERSION: "Mathematics of the Discrete Fourier Transform (DFT), with Audio Applications --- Second Edition", by Julius O. Smith III, W3K Publishing, 2007, ISBN 978-0-9745607-4-8. - Copyright © 2017-09-28 by Julius O. Smith III - Center for Computer Research in Music and Acoustics (CCRMA), Stanford University

<< Previous page  TOC  INDEX  Next page >>

Shift Theorem



Theorem: For any $x\ and any integer $\,

\

Proof:

\



The shift theorem says that a delay in the time domain corresponds to a linear phase term in the frequency domain. More specifically, a delay of $\ samples in the time waveform corresponds to the linear phase term $e^{-j \ multiplying the spectrum, where $\. (To consider $\ as radians per second instead of radians per sample, just replace $\ by $\ so that the delay is in seconds instead of samples.) Note that spectral magnitude is unaffected by a linear phase term. That is, $\.


Subsections

<< Previous page  TOC  INDEX  Next page >>