Vector Addition

GUIDE: Mathematics of the Discrete Fourier Transform (DFT) - Julius O. Smith III. Vector Addition

It appears that you are using AdBlocking software. The cost of running this website is covered by advertisements. If you like it please feel free to a small amount of money to secure the future of this website.
​

NOTE: THIS DOCUMENT IS OBSOLETE, PLEASE CHECK THE NEW VERSION: "Mathematics of the Discrete Fourier Transform (DFT), with Audio Applications --- Second Edition", by Julius O. Smith III, W3K Publishing, 2007, ISBN 978-0-9745607-4-8. - Copyright © 2017-09-28 by Julius O. Smith III - Center for Computer Research in Music and Acoustics (CCRMA), Stanford University

<< Previous page  TOC  INDEX  Next page >>

Vector Addition

Given two vectors in ${\, say $\ and $\, the vector sum is defined byelementwise addition. If we denote the sum by $w\, then we have $w(n) = x(n)+y(n)$ for $n=0,1,2,\.

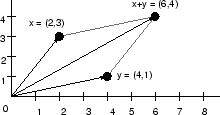
The vector diagram for the sum of two vectors can be found using the parallelogram rule, as shown in Fig. 6.2 for $N=2$, $x=(2, 3)$, and$y=(4,1)$.

Figure 6.2:Geometric interpretation of a length 2 vector sum.
\

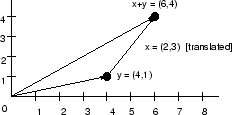
Also shown are the lighter construction lines which complete the parallelogram started by $x$ and $y$, indicating where the endpoint of the sum $x+y$ lies. Since it is a parallelogram, the two construction lines are congruent to the vectors $x$ and $y$. As a result, the vector sum is often expressed as a triangle by translating the origin of one member of the sum to the tip of the other, as shown in Fig. 6.3.

Figure 6.3:Vector sum with translation of one vector to the tip of the other.
\

In the figure, $x$ was translated to the tip of $y$. It is equally valid to translate $y$ to the tip of $x$, because vector addition is commutative, i.e., $x+y$ = $y+x$.

<< Previous page  TOC  INDEX  Next page >>

​
 
​
© 1998-2023 – Nicola Asuni - Tecnick.com - All rights reserved.
about - disclaimer - privacy