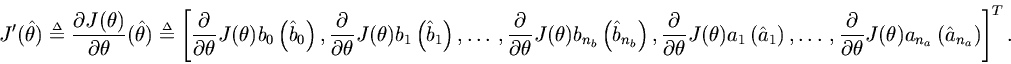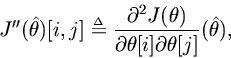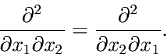18. Gradient Descent

01 Mar 1998

NOTE: THIS DOCUMENT IS OBSOLETE, PLEASE CHECK THE NEW VERSION: "Introduction to Digital Filters with Audio Applications", by Julius O. Smith III, Copyright © 2017-11-26 by Julius O. Smith III - Center for Computer Research in Music and Acoustics (CCRMA), Stanford University

<< Previous page TOC INDEX Next page >>

Gradient Descent

Concavity is valuable in connection with the Gradient Method of minimizing $$J({\$ with respect to $${\$ .

Definition. The gradient of the error measure $$J({\$ is defined as the $${\$ column vector

Definition. The Gradient Method (Cauchy) is defined as follows.

Given $${\$ , compute

where $${J^\$ is the gradient of at $${\$ , and $$t_n\$ is chosen as the smallest nonnegative local minimizer of

Cauchy originally proposed to find the value of $$t_n\$ which gave a global minimum of $$\$ . This, however, is not always feasible in practice.
Some general results regarding the Gradient Method are given below.

Theorem. If $${\$ is a local minimizer of $$J({\$ , and $${J^\$ exists, then $${J^\$ .

Theorem. The gradient method is a descent method, i.e., $$J({\$ .

Definition. $$J:{\$ , $${\$ , is said to be in the class $${\$ if all th order partial derivatives of $$J({\$ with respect to the components of $${\$ are continuous on $${\$ .

Definition. The Hessian $${J^{\$ of at $${\$ is defined as the matrixof second-order partial derivatives,

where $$\$ denotes the th component of $$\$ , $$i=1,\$ , and denotes the matrix entry at the th row and th column.
The Hessian of every element of $${\$ is a symmetric matrix [Williamson et al. 1972]. This is because continuous second-order partials satisfy

Theorem. If $$J\$ , then any cluster point $${\$ of the gradient sequence $${\$ is necessarily astationary point, i.e., $${J^\$ .

Theorem. Let $$\$ denote the concave hull of $${\$ . If $$J\$ , and there exist positive constants and such that

for all $${\$ and for all $$\$ , then the gradient method beginning with any point in $${\$ converges to a point $${\$ . Moreover, $${\$ is the unique global minimizer of in $$\$ .
By the norm equivalence theorem [Ortega 1972], Eq. (5) is satisfied whenever $${J^{\$ is a norm on $${\$ for each $${\$ . Since $${J^{\$ belongs to $${\$ , it is a symmetric matrix. It is also bounded since it is continuous over a compact set. Thus a sufficient requirement is that $${J^{\$ be positive definite on $${\$ . Positive definiteness of $${J^{\$ can be viewed as ``positive curvature'' of at each point of $${\$ which corresponds to strict concavity of on $${\$ .

<< Previous page TOC INDEX Next page >>

GUIDE: Elementary Digital Filter Theory - Julius O. Smith III. Gradient Descent

Gradient Descent