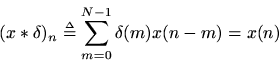NOTE: THIS DOCUMENT IS OBSOLETE, PLEASE CHECK THE NEW VERSION: "Mathematics of the Discrete Fourier Transform (DFT), with Audio Applications --- Second Edition", by Julius O. Smith III, W3K Publishing, 2007, ISBN 978-0-9745607-4-8. - Copyright © 2017-09-28 by Julius O. Smith III - Center for Computer Research in Music and Acoustics (CCRMA), Stanford University

<< Previous page  TOC  INDEX  Next page >>

Appendix A: Linear Time-Invariant Filters and Convolution

A reason for the importance of convolution is that every linear time-invariant system^8.9 can be represented by a convolution. Thus, in the convolution equation

we may interpret as the input signal to a filter, as the output signal, and as the digital filter, as shown in Fig. 8.11.

Figure 8.11:The filter interpretation of convolution.

The impulse or ''unit pulse'' signal is defined by

For example, for , . The impulse signal is the identity element under convolution, since

If we set in the filter equation above, we get

Thus, is the impulse response of the filter.

It turns out in general that every linear time-invariant (LTI) system (filter) is completely described by its impulse response. No matter what the LTI system is, we can give it an impulse, record what comes out, call it , and implement the system by convolving the input signal with the impulse response . In other words, every LTI system has a convolution representation in terms of its impulse response.

---

Subsections

• LTI Filters and the Convolution Theorem

<< Previous page  TOC  INDEX  Next page >>