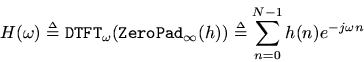LTI Filters and the Convolution Theorem

NOTE: THIS DOCUMENT IS OBSOLETE, PLEASE CHECK THE NEW VERSION: "Mathematics of the Discrete Fourier Transform (DFT), with Audio Applications --- Second Edition", by Julius O. Smith III, W3K Publishing, 2007, ISBN 978-0-9745607-4-8. - Copyright © 2017-09-28 by Julius O. Smith III - Center for Computer Research in Music and Acoustics (CCRMA), Stanford University

<< Previous page  TOC  INDEX  Next page >>

LTI Filters and the Convolution Theorem

Definition: The frequency response of an LTI filter is defined as the Fourier transform of its impulse response. In particular, for finite, discrete-time signals , the sampled frequency response is defined as

The complete frequency response is defined using the DTFT, i.e.,

where we used the fact that is zero for and to truncate the summation limits. Thus, the infinitely zero-padded DTFT can be obtained from the DFT by simply replacing by . In principle, the continuous frequency response is being obtained using ''time-limited interpolation in the frequency domain'' based on the samples . This interpolation is possible only when the frequency samples are sufficiently dense: for a length finite-impulse-response (FIR) filter , we require at least samples around the unit circle (length DFT) in order that be sufficiently well sampled in the frequency domain. This is of course the dual of the usual sampling rate requirement in the time domain.^8.10

Definition: The amplitude response of a filter is defined as the magnitude of the frequency response

From the convolution theorem, we can see that the amplitude response is the gain of the filter at frequency , since

Definition: The phase response of a filter is defined as the phase of the frequency response

From the convolution theorem, we can see that the phase response is the phase-shift added by the filter to an input sinusoidal component at frequency , since

The subject of this section is developed in detail in [1].

<< Previous page  TOC  INDEX  Next page >>