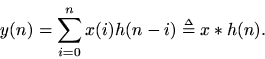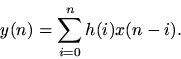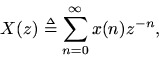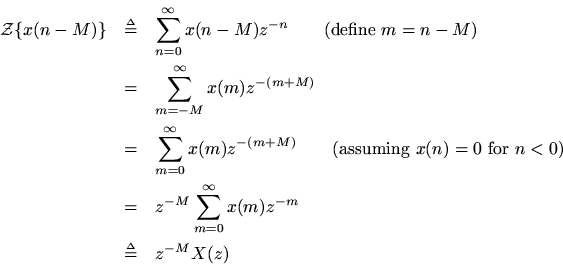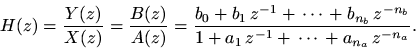Convolution Representation of LTI Filters

NOTE: THIS DOCUMENT IS OBSOLETE, PLEASE CHECK THE NEW VERSION: "Mathematics of the Discrete Fourier Transform (DFT), with Audio Applications --- Second Edition", by Julius O. Smith III, W3K Publishing, 2007, ISBN 978-0-9745607-4-8. - Copyright © 2017-09-28 by Julius O. Smith III - Center for Computer Research in Music and Acoustics (CCRMA), Stanford University

<< Previous page  TOC  INDEX  Next page >>

Convolution Representation of LTI Filters

If is the output of an LTI filter with input and impulse response , then is the convolution of with ,

Since convolution is commutative (), we have also

Definition. The unilateral transform of the discrete-time signal is defined to be

(B.9)

That and are transform pairs is expressed by writing or .

Theorem. The convolution theorem (Papoulis [21]) states that

In words, convolution in the time domain is multiplication in the frequency domain.

Taking the transform of both sides of Eq. (B.4.3) and applying the convolution theorem gives

where is the transform of the filter impulse response. Thus the transform of the filter output is the transform of the input times the transform of the impulse response.

Definition. The transfer function of a linear time-invariant discrete-time filter is defined to be the transform of the impulse response .

Theorem. The shift theorem [21] for transforms states that

The shift theorem can be derived immediately from the definition of the transformgiven in Eq. ():

The general difference equation for an LTI filter appears as

			(B.10)
			(B.11)

Taking the transform of both sides, denoting the transform by , gives

			(B.12)
			(B.13)

using linearity and the shift theorem. Replacing by , by , and moving the terms in to the left-hand side, we obtain

			(B.14)
			(B.15)

or

			(B.16)
			(B.17)

Defining the polynomials

			(B.18)
			(B.19)

the transform of the difference equation becomes

Finally, solving for which equals the transfer function , yields

<< Previous page  TOC  INDEX  Next page >>