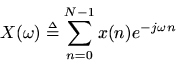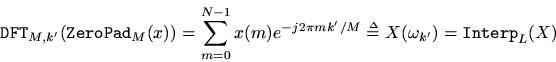Zero Padding Theorem

NOTE: THIS DOCUMENT IS OBSOLETE, PLEASE CHECK THE NEW VERSION: "Mathematics of the Discrete Fourier Transform (DFT), with Audio Applications --- Second Edition", by Julius O. Smith III, W3K Publishing, 2007, ISBN 978-0-9745607-4-8. - Copyright © 2017-09-28 by Julius O. Smith III - Center for Computer Research in Music and Acoustics (CCRMA), Stanford University

<< Previous page  TOC  INDEX  Next page >>

Zero Padding Theorem

A fundamental tool in practical spectrum analysis is zero padding. This theorem shows that zero padding in the time domain corresponds to ideal interpolation in the frequency domain:

Let and define . Then with . Denote the original frequency index by , where and the new frequency index by , where .

Definition: The ideal bandlimited interpolation of a spectrum , , to an arbitrary new frequency is defined as

Note that this is just the definition of the DFT with replaced by . That is, the spectrum is interpolated by projecting onto the new sinusoid exactly as if it were a DFT sinusoid. This makes the most sense when is assumed to be samples of a time-limited signal. That is, if the signal really is zero outside of the time interval, then the inner product between it and any sinusoid will be exactly as in the equation above. Thus, for time limited signals, this kind of interpolation is ideal.

Definition: The interpolation operator interpolates a signal by an integer factor. That is,

Since is initially only defined over the roots of unity, while is defined over roots of unity, we define for by ideal bandlimited interpolation.

Theorem: For any

Proof: Let with . Then

<< Previous page  TOC  INDEX  Next page >>