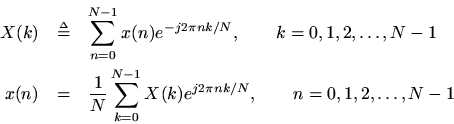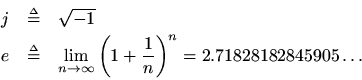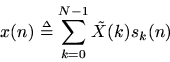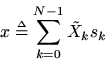NOTE: THIS DOCUMENT IS OBSOLETE, PLEASE CHECK THE NEW VERSION: "Mathematics of the Discrete Fourier Transform (DFT), with Audio Applications --- Second Edition", by Julius O. Smith III, W3K Publishing, 2007, ISBN 978-0-9745607-4-8. - Copyright © 2017-09-28 by Julius O. Smith III - Center for Computer Research in Music and Acoustics (CCRMA), Stanford University

<< Previous page  TOC  INDEX  Next page >>

Mathematics of the DFT

In the signal processing literature, it is common to write the DFT in the more pure form obtained by setting in the previous definition:

where denotes the input signal at time (sample) , and denotes the th spectral sample.^1.1 This form is the simplest mathematically while the previous form is the easier to think about physically.

There are two remaining symbols in the DFT that we have not yet defined:

The first, , is the basis for complex numbers. As a result, complex numbers will be the first topic we cover in this course (but only to the extent needed to understand the DFT).

The second, , is a transcendental number defined by the above limit. In this course we will derive and talk about why it comes up.

Note that not only do we have complex numbers to contend with, but we have them appearing in exponents, as in

We will systematically develop what we mean by imaginary exponents in order that such mathematical expressions are well defined.

With , , and imaginary exponents understood, we can go on to prove Euler's Identity:

Euler's Identity is the key to understanding the meaning of expressions like

We'll see that such an expression defines a sampled complexsinusoid, and we'll talk about sinusoids in some detail, from an audio perspective.

Finally, we need to understand what the summation over is doing in the definition of the DFT. We'll learn that it should be seen as the computation of the inner product of the signals and , so that we may write the DFT using inner-product notation as

where

is the sampled complex sinusoid at (normalized) radian frequency , and the inner product operation is defined by

We will show that the inner product of with the th ''basis sinusoid'' is a measure of ''how much'' of is present in and at ''what phase'' (since it is a complex number).

After the foregoing, the inverse DFT can be understood as theweighted sum of projections of onto , i.e.,

where

is the (actual) coefficient of projection of onto . Referring to the whole signal as a whole, the IDFT can be written as

Note that both the basis sinusoids and their coefficients of projection are complex.

Having completely understood the DFT and its inverse mathematically, we go on to proving various Fourier Theorems, such as the ''shift theorem,'' the ''convolution theorem,'' and ''Parsevals' theorem.'' The Fourier theorems provide a basic thinking vocabulary for working with signals in the time and frequency domains. They can be used to answer questions like

What happens in the frequency domain if I do this in the time domain?

In the remaining class time, we will study a variety of practical spectrum analysis examples, using primarily Matlab to analyze and display signals and their spectra.

<< Previous page  TOC  INDEX  Next page >>