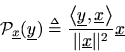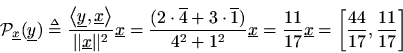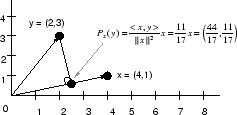Projection

01 Mar 1998

NOTE: THIS DOCUMENT IS OBSOLETE, PLEASE CHECK THE NEW VERSION: "Mathematics of the Discrete Fourier Transform (DFT), with Audio Applications --- Second Edition", by Julius O. Smith III, W3K Publishing, 2007, ISBN 978-0-9745607-4-8. - Copyright © 2017-09-28 by Julius O. Smith III - Center for Computer Research in Music and Acoustics (CCRMA), Stanford University

<< Previous page TOC INDEX Next page >>

Projection

The orthogonal projection (or simply ''projection'') of $$\$ onto $$\$ is defined by

The complex scalar $$\$ is called thecoefficient of projection. When projecting $$\$ onto a unit length vector $$\$ , the coefficient of projection is simply the inner product of $$\$ with $$\$ .
Motivation: The basic idea of orthogonal projection of $$\$ onto $$\$ is to ''drop a perpendicular'' from $$\$ onto $$\$ to define a new vector along $$\$ which we call the ''projection'' of $$\$ onto $$\$ . This is illustrated for in Fig. 6.9 for $$\$ and $$\$ , in which case

Figure 6.9:Projection of $$\$ onto $$\$ in 2D space.

Derivation: (1) Since any projection onto $$\$ must lie along the line colinear with $$\$ , write the projection as $${\$ . (2) Since by definition the projection is orthogonal to $$\$ , we must have

<< Previous page TOC INDEX Next page >>

GUIDE: Mathematics of the Discrete Fourier Transform (DFT) - Julius O. Smith III. Projection

Projection