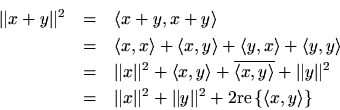The Pythagorean Theorem in N-Space

NOTE: THIS DOCUMENT IS OBSOLETE, PLEASE CHECK THE NEW VERSION: "Mathematics of the Discrete Fourier Transform (DFT), with Audio Applications --- Second Edition", by Julius O. Smith III, W3K Publishing, 2007, ISBN 978-0-9745607-4-8. - Copyright © 2017-09-28 by Julius O. Smith III - Center for Computer Research in Music and Acoustics (CCRMA), Stanford University

<< Previous page  TOC  INDEX  Next page >>

The Pythagorean Theorem in N-Space

In 2D, the Pythagorean Theorem says that when and are orthogonal, as in Fig. 6.8, (i.e., when the triangle formed by , , and , with translated to the tip of , is a right triangle), then we have

This relationship generalizes to dimensions, as we can easily show:

If , then and the Pythagorean Theorem holds in dimensions. If, on the other hand, we assume the Pythagorean Theorem holds, then since all norms are positive unless or is zero, we must have . Finally, if or is zero, the result holds trivially.

Note that we also have an alternate version of the Pythagorean theorem:

<< Previous page  TOC  INDEX  Next page >>