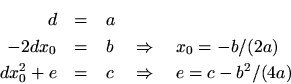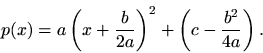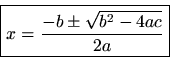NOTE: THIS DOCUMENT IS OBSOLETE, PLEASE CHECK THE NEW VERSION: "Mathematics of the Discrete Fourier Transform (DFT), with Audio Applications --- Second Edition", by Julius O. Smith III, W3K Publishing, 2007, ISBN 978-0-9745607-4-8. - Copyright © 2017-09-28 by Julius O. Smith III - Center for Computer Research in Music and Acoustics (CCRMA), Stanford University

<< Previous page  TOC  INDEX  Next page >>

The Quadratic Formula

The general second-order polynomial is

where the coefficients are any real numbers, and we assume since otherwise it would not be second order. Some experiments plotting for different values of the coefficients leads one to guess that the curve is always a scaled and translated parabola. The canonical parabola centered at is given by

where determines the width and provides an arbitrary vertical offset. If we can find in terms of for any quadratic polynomial, then we can easily factor the polynomial. This is called ''completing the square.'' Multiplying out , we get

Equating coefficients of like powers of gives

Using these answers, any second-order polynomial can be rewritten as a scaled, translated parabola

In this form, the roots are easily found by solving to get

This is the general quadratic formula. It was obtained by simple algebraic manipulation of the original polynomial. There is only one ''catch.'' What happens when is negative? This introduces the square root of a negative number which we could insist ''does not exist.'' Alternatively, we could invent complex numbers to accommodate it.

<< Previous page  TOC  INDEX  Next page >>