Reconstruction from Samples--Pictorial Version

NOTE: THIS DOCUMENT IS OBSOLETE, PLEASE CHECK THE NEW VERSION: "Mathematics of the Discrete Fourier Transform (DFT), with Audio Applications --- Second Edition", by Julius O. Smith III, W3K Publishing, 2007, ISBN 978-0-9745607-4-8. - Copyright © 2017-09-28 by Julius O. Smith III - Center for Computer Research in Music and Acoustics (CCRMA), Stanford University

<< Previous page  TOC  INDEX  Next page >>

Reconstruction from Samples--Pictorial Version

Figure A.1 shows how a sound is reconstructed from its samples. Each sample can be considered as specifying thescaling and location of a sinc function. The discrete-time signal being interpolated in the figure is . The sinc functions are drawn with dashed lines, and they sum to produce the solid curve. Note the ''Gibb's overshoot'' near the corners of this continuous rectangular pulse due to band-limiting.

Figure A.1:How sinc functions sum up to create a continuous waveform from discrete-time samples.

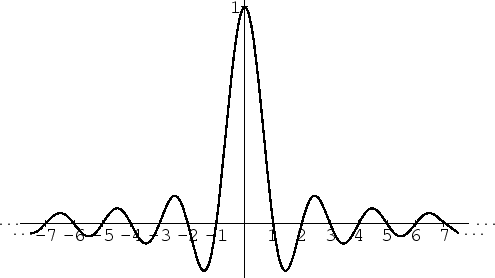
Note how each sinc function passes through zero at every sample instant but the one it is centered on, where it passes through 1. An isolated sinc function is shown in Fig. A.2.

Figure A.2:The sinc function.

The sinc function is the famous ''sine x over x'' curve, defined by

where denotes the sampling rate in samples-per-second, and denotes time in seconds.

<< Previous page  TOC  INDEX  Next page >>