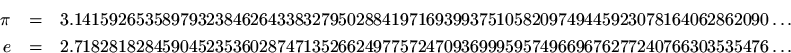Real Exponents

NOTE: THIS DOCUMENT IS OBSOLETE, PLEASE CHECK THE NEW VERSION: "Mathematics of the Discrete Fourier Transform (DFT), with Audio Applications --- Second Edition", by Julius O. Smith III, W3K Publishing, 2007, ISBN 978-0-9745607-4-8. - Copyright © 2017-09-28 by Julius O. Smith III - Center for Computer Research in Music and Acoustics (CCRMA), Stanford University

<< Previous page  TOC  INDEX  Next page >>

Real Exponents

The closest we can actually get to most real numbers is to compute arational number that is as close as we need. It can be shown that rational numbers are dense in the real numbers; that is, between every two real numbers there is a rational number, and between every two rational numbers is a real number. Anirrational number can be defined as any real number having a non-repeating decimal expansion. For example, is an irrational real number whose decimal expansion starts out as

(computed via N[Sqrt[2],80] in Mathematica). Every truncated, rounded, or repeating expansion is a rational number. That is, it can be rewritten as an integer divided by another integer. For example,

and, using to denote the repeating part of a decimal expansion,

Other examples of irrational numbers include

Let denote the -digit decimal expansion of an arbitrary real number . Then is a rational number (some integer over ). We can say

Since is defined for all , it is straightforward to define

<< Previous page  TOC  INDEX  Next page >>