NOTE: THIS DOCUMENT IS OBSOLETE, PLEASE CHECK THE NEW VERSION: "Mathematics of the Discrete Fourier Transform (DFT), with Audio Applications --- Second Edition", by Julius O. Smith III, W3K Publishing, 2007, ISBN 978-0-9745607-4-8. - Copyright © 2017-09-28 by Julius O. Smith III - Center for Computer Research in Music and Acoustics (CCRMA), Stanford University
<< Previous page TOC INDEX Next page >>
Zero Padding
Definition: Zero padding consists of appending zeros to a signal. It maps a lengthsignal to a length
signal, but
need not be an integer multiple of
For example,
The above definition is natural whenrepresents a signal starting at time
and extending for
and
for
), and similarly for even
(
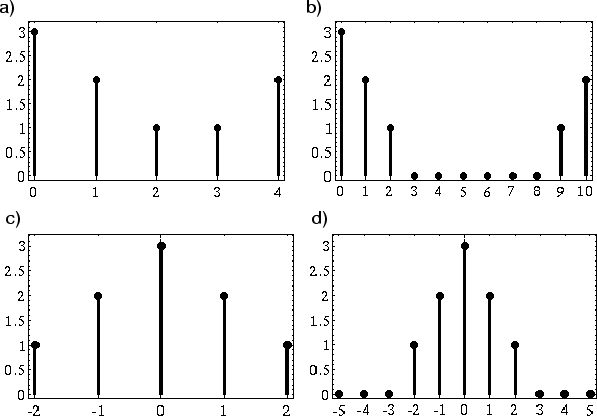
). Figure 8.5 illustrates this second form of zero padding. It is also used in conjunction with zero-phase FFT windows(discussed a bit further below).
Figure 8.5:Illustration of frequency-domain zero padding: a) Original spectrum plotted over the domain
where
(i.e., as the spectral array would normally exist in a computer array). b)
. c) The same signal
plotted over the domain
which is more natural for interpreting negative frequencies. d)
Using Fourier theorems, we will be able to show that zero padding in the time domain gives bandlimited interpolation in the frequency domain. Similarly, zero padding in the frequency domain gives bandlimited interpolation in the time domain. This is how ideal sampling rate conversion is accomplished.
It is important to note that bandlimited interpolation is idealinterpolation in digital signal processing.
