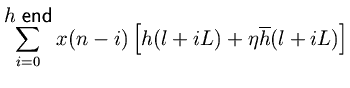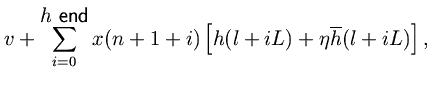Implementation
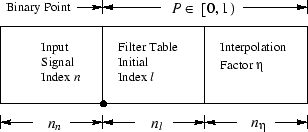
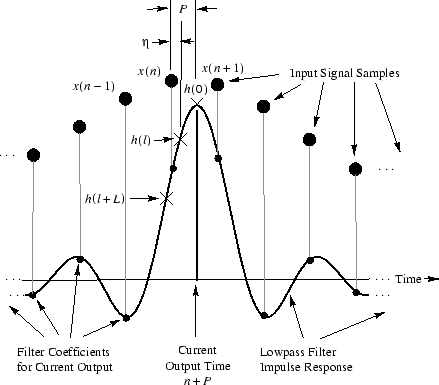
Our implementation provides signal evaluation at an arbitrary
time, where time is specified as an unsigned binary fixed-point number in units of the input
sampling period (assumed constant).
Figure 6
shows the time register 
, and Figure 7
shows an example configuration of the input signal and lowpass
filter at
a given time. The time register is divided into three fields: The
leftmost field gives the number 
of samples into the input signal buffer, the middle field is an
initial index 
into the filter coefficient table 
, and the rightmost field is interpreted as a number
between 
and 
for doinglinear interpolation between samples
and 
(initially) of the filter table. The concatenation of
and are called
which is interpreted as the position of the current
time between samples
and 
of the input signal.
Let the three fields have 
, 
, and 
bits, respectively. Then the input signal buffer
contains 
samples, and the filter table contains 
``samples per zero-crossing.'' (The term
``zero-crossing'' is precise only for the case of the ideal
lowpass; to cover practical cases we generalize ``zero-crossing''
to mean a multiple of time 
, where 
is the lowpass cutoff frequency.) For example, to use the ideal lowpass
filter, the table would contain 
.
Our implementation stores only the ``right wing'' of a symmetric
finite-impulse-response
(FIR) filter (designed by the window method based on a Kaiser
window [Rabiner
and Gold 1975]). It also stores a table of differences
between successive FIR sample values in order to
speed up the linear interpolation. The length of each table is then
.
Consider a sampling-rate
conversion by the factor 
. For each output sample, the basic
interpolation Eq. (1) is
performed. The filter table is traversed twice--first to apply the
left wing of the FIR filter, and second to apply the right wing.
After each output sample is computed, the time register is
incremented by 
(i.e., time is incremented by
in fixed-point format). Suppose the time register
has just been updated, and an interpolated output 
is desired. For
,
output is computed via
where 
is the current input sample, and 
is the interpolation factor. When 
, the initial 
is replaced by
, 
becomes 
, and the step-size through the filter table is
reduced to 
instead of 
;
this lowers the filter cutoff to avoid aliasing. Note that is fixed throughout the computation of an output sample when
but changes when .
Figure 6:Time register
format.
|
|
Figure 7:Illustration of
waveforms and parameters in the interpolator.
|
|
When , more input samples are required to reach the end of
the filter table, thus preserving the filtering quality. The number
of multiply-adds per second is approximately 
. Thus the higher sampling rate determines the work rate. Note
that for there must be 
extra input samples available before
the initial conversion time and after the final conversion time in
the input buffer. As 
,
the required extra input data becomes infinite, and some limit must
be chosen, thus setting a minimum supported
. For , only 
extra input samples are required on the left and right of
the data to be resampled, and the
upper bound for is determined only by the fixed-point number
format, viz., 
.
As shown below, if 
denotes the word-length of the stored impulse-response
samples, then one may choose 
, and 
to obtain 
effective bits of precision in the interpolated
impulse response.
Note that rational conversion factors of the form 
, where and 
is an arbitrary positive integer, do not use the linear
interpolation feature (because 
). In this case our method reduces to the normal
type of bandlimited interpolator [Crochiere
and Rabiner 1983]. With the availability of interpolated
lookup, however, the range of conversion factors is boosted to the
order of 
. E.g., for
,
, this is about 
decimal digits of accuracy in the conversion factor
. Without interpolation, the number of significant figures in
is only about 
.
The number of zero-crossings stored in the table is an independent
design parameter. For a given quality specification in terms of
aliasing rejection, a trade-off exists between and sacrificed bandwidth. The lost bandwidth is due to the
so-called ``transition band'' of the lowpass filter [Rabiner
and Gold 1975]. In general, for a given stop-band
specification (such as ``80 dB attenuation''), lowpass filters need approximately
twice as many multiply-adds per sample for each halving of the
transition band width.
As a practical design example, we use 
in a system designed for high audio quality at
% oversampling. Thus, the effective FIR filter is
zero crossings long. The sampling rate in this case would
be 
kHz.1In the most straightforward filter design, the lowpass filter pass-band
would stop and the transition-band would begin at kHz, and the stop-band would begin (and end) at 
kHz. As a further refinement, which reduces the filter
design requirements, the transition band is really designed to
extend from kHz to 
kHz, so that the half of it between and kHz aliases on top of the half between and kHz, thereby approximately halving the filter length
required. Since the entire transition band lies above the range of
human hearing, aliasing within it is not audible.
Using 
samples per zero-crossing in the filter table for the
above example (which is what we use at CCRMA, and
which is somewhat over designed) implies desiging a length
FIR filter having a cut-off frequency near
. It turns out that optimal Chebyshev design procedures such
as the Remez multiple exchange algorithm used in the Parks-McLellan
software [Rabiner
and Gold 1975] can only handle filter lengths up to a
couple hundred or so. It is therefore necessary to use an FIR filter design method which works well at
such very high orders, and the window method employed here is one
such method.
It is worth noting that a given percentage increase in the
original sampling rate (``oversampling'') gives a larger percentage
savings in filter computation time, for a given quality
specification, because the added bandwidth is a larger percentage
of the filter transition bandwidth than it is of the original
sampling rate. For example, given a cut-off frequency of
kHz, (ideal for audio work), the transition band available
with a sampling rate of 
kHz is about 
kHz, while a
kHz sampling rate provides a 
kHz transition band. Thus, a
% increase in sampling rate halves the work per
sample in the digital lowpass filter.
