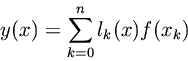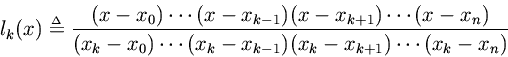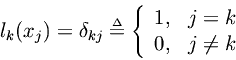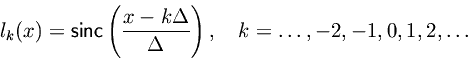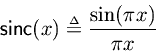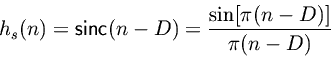14. Appendix B: Relation between Sinc and Lagrange Interpolation

01 Mar 1998

NOTE: THIS DOCUMENT IS OBSOLETE, PLEASE CHECK THE NEW VERSION: "The Digital Audio Resampling Home Page", by Julius O. Smith III, Copyright © 2016-05-17 by Julius O. Smith III - Center for Computer Research in Music and Acoustics (CCRMA), Stanford University

<< Previous page TOC Next page >>

Appendix B: Relation between Sinc and Lagrange Interpolation

Lagrange interpolation is a well known, classical technique for interpolation [Hildebrand 1974]. Given a set of known samples, $$k=0,1,2,\$ , the problem is to find the unique order polynomial which interpolates the samples. The solution can be expressed as a linear combination of elementary th order polynomials:

where

From the numerator of the above definition, we see that is an order polynomial having zeros at all of the samples except the th. The denominator is simply the constant which normalizes its value to at. Thus, we have

In other words, the polynomial is the th basis polynomial for constructing a polynomial interpolation of order over the sample points .
In the case of an infinite number of equally spaced samples, with spacing $$x_{k+1}-x_k = \$ , the Lagrangian basis polynomials converge to shifts of the sinc function, i.e.,

where

The simplest argument is based on the fact that any analytic function is determined by its zeros and its value at one point. Since $$\$ is zero on all the integers except , and since $$\$ , it must coincide with the infinite-order Lagrangian basis polynomial for the sample at which also has its zeros on the nonzero integers and equals at.
A direct proof can be based on the equivalance between Lagrange interpolation and windowed-sinc interpolation using a ``binomial window'' [Kootsookos and Williamson 1996,Välimäki 1995]. That is, for a fractional sample delay of samples, multiply the shifted-by-, sampled, sinc function

by a binomial window

and normalize by [Välimäki 1995]

which normalizes the interpolating filter to have a unit norm, to obtain the th-order Lagrange interpolating filter

Since the binomial window converges to the Gaussian window as $$N\$ , and since the window gets wider and wider, approaching a unit constant in the limit, the convergence of Lagrange to sinc interpolation can be seen.