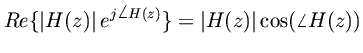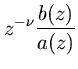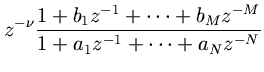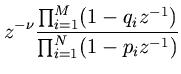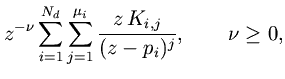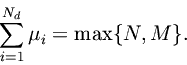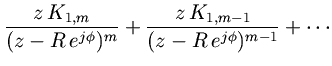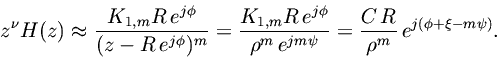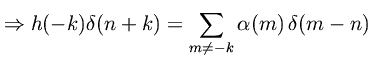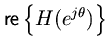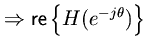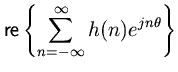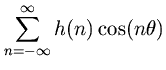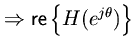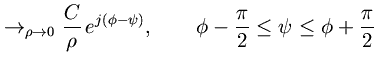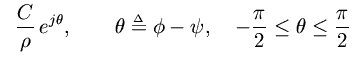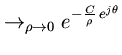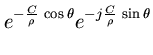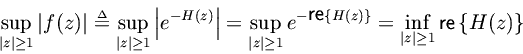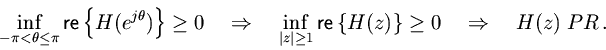01. Positive Real Functions

01 Mar 1998

NOTE: THIS DOCUMENT IS OBSOLETE, PLEASE CHECK THE NEW VERSION: "Introduction to Digital Filters with Audio Applications", by Julius O. Smith III, Copyright © 2017-11-26 by Julius O. Smith III - Center for Computer Research in Music and Acoustics (CCRMA), Stanford University

<< Previous page TOC INDEX Next page >>

Positive Real Functions

Any passive driving-point impedance, such as the impedance of a violin bridge, is positive real. Positive real functions have been studied extensively in the continuous-time case in the context ofnetwork synthesis [Brune 1931,Van Valkenburg 1960]. Very little, however, seems to be available in the discrete time case. The purpose of this home page is to collect some facts about positive real transfer functions for discrete-time linear systems.

Definition. A complex valued function of a complex variable is said to bepositive real (PR) if

$$z real \$

$$\$

We now specialize to the subset of functions representable as a ratio of finite-order polynomials in . This class of ``rational'' functions is the set of all transfer functions of finite-order time-invariant linear systems, and we write to denote a member of this class. We use the convention that stable, minimum phase systems are analytic and nonzero in the strict outer disk.¹*The strict outer disk is defined as the region $$\$ in the extended complex plane. Condition (1) implies that for to be PR, the polynomial coefficients must be real, and therefore complex poles and zeros must exist in conjugate pairs. We assume from this point on that $$H(z)\$ satisfies (1). From (2) we derive the facts below.

Theorem. A real rational function is PR iff $$\$ .

Proof. Expressing in polar form gives

$$\$ $$\$ $$\$ (1)

$$\$ (2)

since the zeros of are isolated. $$\$
Theorem. is PR iff is PR.

Proof. Assuming is PR, we have by Thm. (1),

$$\$
Theorem. A PR function is analytic and nonzero in the strict outer disk.

Proof. (By contradiction)

Without loss of generality, we treat only $n^{th}$ order polynomials

which are nondegenerate in the sense that $$\$ . Since facts about $$\$ are readily deduced from facts about , we set $$\$ at no great loss.
The general (normalized) causal, finite-order, linear, time-invariant transfer function may be written

$$\$ $$\$ $$\$ (3)

$$\$ $$\$ (4)

$$\$ $$\$ (5)

$$\$ $$\$ (6)

where is the number of distinct poles, each of multiplicity $$\$ ,and

Suppose there is a pole of multiplicity outside the unit circle. Without loss of generality, we may set $$\$ , and $$p_1 = R e^{j\$ with . Then for near , we have

$$\$ $$\$ $$\$ (7)

$$\$ (8)

Consider the circular neighborhood of radius $$\$ described by $$z=R e^{j\$ . Since we may choose $$\$ so that all points in this neighborhood lie outside the unit circle. If we write the residue of the factor $$(z-R e^{j\$ in polar form as $$K_{1,m}=C e^{j\$ , then we have, for sufficiently small $$\$ ,

Therefore, approaching the pole $$R e^{j\$ at an angle $$\$ gives

which cannot be confined to satisfy Thm. (1) regardless of the value of the residue angle $$\$ , or the pole angle $$\$ ( cannot be zero by hypothesis). We thus conclude that a PR function can have no poles in the outer disk. By Thm. (1), we conclude that positive real functions must be minimum phase. $$\$
Corollary. In equation Eq. (6), $$\$ .

Proof. If $$\$ , then there are $$\$ poles at infinity. As $$\$ , $$H(z)\$ , we must have $$\$ . $$\$

Corollary. The log-magnitude of a PR function has zero mean on the unit circle.

This is a general property of stable, minimum-phase transfer functions which follows immediately from the argument principle [Markel and Gray 1976,Nehari 1952].

Corollary. A rational PR function has an equal number of poles and zeros all of which are in the unit disk.

This really a convention for numbering poles and zeros. In Eq. (6), we have $$\$ , and all poles and zeros inside the unit disk. Now, if then we have extra poles at induced by the numerator. If , then zeros at the origin appear from the denominator.

Corollary. Every pole on the unit circle of a positive real function must be simple with a real and positive residue.

Proof. We repeat the previous argument using a semicircular neighborhood of radius $$\$ about the point $$p_1 = e^{j\$ to obtain

In order to have $$\$ near this pole, it is necessary that and $$\$ . $$\$
Corollary. If is PR with a zero at $$z=q_1=e^{j\$ , then

must satisfy

$$\$ $$\$ $$\$ (9)

$$\$ $$\$ $$\$ (10)

Proof. We may repeat the above for .

Theorem. Every PR function has a causal inverse -transform .

Proof. This follows immediately from analyticity in the outer disk [Papoulis 1977, pp. 30-36] However, we may give a more concrete proof as follows. Suppose is non-causal. Then there exists such that $$h(-k)\$ . We have,

$$\$ $$\$ $$\$ (11)

$$\$ $$\$ (12)

Hence, has at least one pole at infinity and cannot be PR by Thm. (1). Note that this pole at infinity cannot be cancelled since otherwise

$$\$ (13)

$$\$ (14)

$$\$ (15)

which contradicts the hypothesis that is non-causal. $$\$
Theorem. is PR iff it is analytic for $$\$ , poles on the unit circle are simple with real and positive residues, and $$Re\$ for $$0\$ .

Proof. If is positive real, the conditions stated hold by virtue of Thm. (1) and the definition of positive real.

To prove the converse, we first show nonnegativity on the upper semicircle implies nonnegativity over the entire circle.

$$\$ $$\$ $$\$ (16)

$$\$ $$\$ $$\$ (17)

$$\$ $$\$ (18)

$$\$ $$\$ (19)

$$\$ (20)

$$\$ $$\$ (21)

Alternatively, we might simply state that real $$\$ even in $$\$ .
Next, since the function is analytic everywhere except at $$z=\$ , it follows that $f(z)=e^{-H(z)}$ is analytic wherever is finite. There are no poles of outside the unit circle due to the analyticity assumption, and poles on the unit circle have real and positive residues. Referring again to the limiting form Eq. (1) of near a pole on the unit circle at $$e^{j\$ , we see that

$$\$ $$\$ (22)

$$\$ $$\$ (23)

$$\$ $$\$ (24)

$$\$ $$\$ (25)

$$\$ (26)

since the residue is positive, and the net angle $$\$ does not exceed $$\$ . From Eq. (26) we can state that for points $$z,z^\$ with modulus $$\$ , we have For all $$\$ , there exists $$\$ such that $$\$ . Thus is analytic in the strict outer disk, and continuous up to the unit circle which forms its boundary. By the maximum modulus theorem [Churchill 1960],

occurs on the unit circle. Consequently,

For example, if a transfer function is known to be asymptotically stable, then a frequency response with nonnegative real part implies that the transfer function is positive real.

Note that consideration of leads to analogous necessary and sufficient conditions for to be positive real in terms of its zeros instead of poles. $$\$