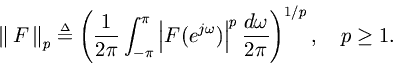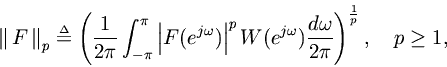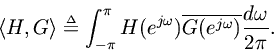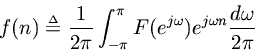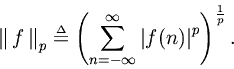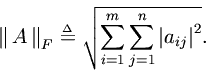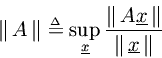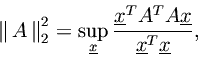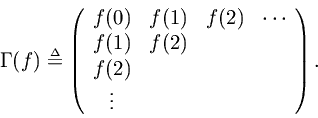15. Specific Norms

01 Mar 1998

NOTE: THIS DOCUMENT IS OBSOLETE, PLEASE CHECK THE NEW VERSION: "Introduction to Digital Filters with Audio Applications", by Julius O. Smith III, Copyright © 2017-11-26 by Julius O. Smith III - Center for Computer Research in Music and Acoustics (CCRMA), Stanford University

<< Previous page TOC INDEX Next page >>

Specific Norms

The norms are defined on the space by

norms are technically pseudo-norms; if functions in are replaced by equivalence classes containing all functions equal almost everywhere, then a norm is obtained.
Since all practical desired frequency responses arising in digital filter design problems are bounded on the unit circle, it follows that $$\$ forms a Banach space under any norm.

The weighted norms are defined by

where $$W(e^{j\$ is real, positive, and integrable. Typically, $$\$ . If $$W(e^{j\$ for a set of nonzero measure, then a pseudo-norm results.
The case gives the popular root mean square norm, and $$ \$ can be interpreted as the total energy of in many physical contexts.

An advantage of working in is that the norm is provided by an inner product,

The norm of a vector $$H\$ is then given by

As approaches infinity in Eq. (3.1), the error measure is dominated by the largest values of $$\$ . Accordingly, it is customary to define

and this is often called the Chebyshev oruniform norm.
Suppose the norm of $$F(e^{j\$ is finite, and let

denote the Fourier coefficients of $$F(e^{j\$ . When $$F(e^{j\$ is afilter frequency response, is the corresponding impulseresponse. The filter is said to be causal if for.
The norms for impulse response sequences $$ \$ are defined in a manner exactly analogous with the frequency response norms $$ \$ , viz.,

These time-domain norms are called norms.
The and norms are strictly concave functionals for $$1<p<\$ (see below).

By Parseval's theorem, we have $$ \$ , i.e., the and norms are the same for .

The Frobenious norm of an $$m\$ matrix is defined as

That is, the Frobenious norm is the norm applied to the elements of the matrix. For this norm there exists the following.
Theorem. The unique $$m\$ rank matrix which minimizes $$ \$ is given by $$U\$ , where $$A=U\$ is a singular value decomposition of , and $$\$ is formed from $$\$ by setting to zero all but the largest singular values.

Proof. See Golub and Kahan [Golub and Van Loan 1989].

The induced norm of a matrix is defined in terms of the norm defined for the vectors $${\$ on which it operates,

For the norm, we have

and this is called the spectral norm of the matrix .
The Hankel matrix corresponding to a time series is defined by $$\$ , i.e.,

Note that the Hankel matrix involves only causal components of the time series.
The Hankel norm of a filter frequency response is defined as the spectral norm of the Hankel matrix of its impulse response,

The Hankel norm is truly a norm only if $$H(z)\$ , i.e., if it is causal. For noncausal filters, it is a pseudo-norm.
If is strictly stable, then $$\$ is finite for all $$\$ , and all norms defined thus far are finite. Also, the Hankel matrix $$\$ is a bounded linear operator in this case.

The Hankel norm is bounded below by the norm, and bounded above by the norm [Genin 1981],

with equality iff is an allpass filter (i.e., $$\$ constant).

<< Previous page TOC INDEX Next page >>

GUIDE: Elementary Digital Filter Theory - Julius O. Smith III. Specific Norms

Specific Norms