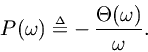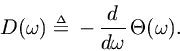13. Phase Delay and Group Delay

01 Mar 1998

NOTE: THIS DOCUMENT IS OBSOLETE, PLEASE CHECK THE NEW VERSION: "Introduction to Digital Filters with Audio Applications", by Julius O. Smith III, Copyright © 2017-11-26 by Julius O. Smith III - Center for Computer Research in Music and Acoustics (CCRMA), Stanford University

<< Previous page TOC INDEX Next page >>

Phase Delay and Group Delay

The phase response of a filter $$\$ gives the radian phase shift experienced by each sinusoidal component of the input signal. Sometimes it is more meaningful to consider phase delay[Papoulis 1977].

Definition. The phase delay of an LTI filter with phase response $$\$ is defined by

The phase delay gives the time delay in seconds experienced by each sinusoidal component of the input signal. For example, in filter $$y(n)\$ , the phase response is $$\$ which corresponds to a phase delay $$P(\$ which is one-half sample.

More generally, if the input to a filter with frequency response $$H(e^{j\$ is

then the output is

and it can be seen that the phase delay expresses phase response as time delay.
In working with phase delay, care must be taken to ensure all appropriate multiples of $$2\$ have been included in $$\$ . We defined $$\$ simply as the complex angle of the frequencyresponse $$H(e^{j\$ , and this is not sufficient for obtaining a phase response which can be converted to true time delay. By discarding multiples of $$2\$ , as is done in the definition of complex angle, the phase delay is modified by multiples of the sinusoidal period. Since LTI filter analysis is based on sinusoids without beginning or end, one cannot in principle distinguish between ``true'' phase delay and a phase delay with discarded sinusoidal periods. Nevertheless, it is convenient to define the filter phase response as a continuous function of frequency with the property that $$\$ (for real filters). This specifies a means of ``unwrapping'' the phase response to get a consistent phase delay curve.

Definition. A more commonly encountered representation of filter phase response is called the group delay, and it is defined by

For linear phase responses, the group delay and the phase delay are identical, and each may be interpreted as time delay.

For any phase function, the group delay $$D(\$ may be interpreted as the time delay of the amplitude envelope of a sinusoid at frequency $$\$ [Papoulis 1977]. The bandwidth of the amplitude envelope in this interpretation must be restricted to a frequency interval over which the phase response is approximately linear. While the proof will not be given here, it should seem reasonable when the process of amplitude envelope detection is considered. The narrow ``bundle'' of frequencies centered at the carrier frequency $$\$ is translated to Hz. At this point, it is evident that the group delay at the carrier frequency gives the slope of the linear phase of the translated spectrum. But this is a constant phase delay, and therefore it has the interpretation of true time delay for the amplitude envelope.

<< Previous page TOC INDEX Next page >>

13. Phase Delay and Group Delay

GUIDE: Elementary Digital Filter Theory - Julius O. Smith III. Phase Delay and Group Delay

Phase Delay and Group Delay