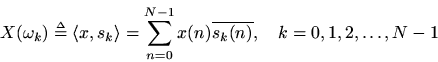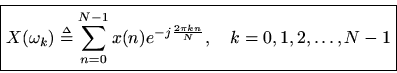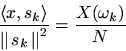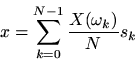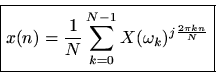The Discrete Fourier Transform (DFT) Derived

NOTE: THIS DOCUMENT IS OBSOLETE, PLEASE CHECK THE NEW VERSION: "Mathematics of the Discrete Fourier Transform (DFT), with Audio Applications --- Second Edition", by Julius O. Smith III, W3K Publishing, 2007, ISBN 978-0-9745607-4-8. - Copyright © 2017-09-28 by Julius O. Smith III - Center for Computer Research in Music and Acoustics (CCRMA), Stanford University

<< Previous page  TOC  INDEX  Next page >>

The Discrete Fourier Transform (DFT)

Given a signal , the spectrum is defined by

or, as is most often written

That is, the th sample of the spectrum of is defined as the inner product of with the th DFT sinusoid . This definition is times the coefficient of projection of onto , i.e.,

The projection of onto itself is

The inverse DFT is simply the sum of the projections:

or, as we normally write,

In summary, the DFT is proportional to the set of coefficients of projection onto the sinusoidal basis set, and the inverse DFT is the reconstruction of the original signal as a superposition of its sinusoidal projections.

---

Subsections

• The DFT Derived
  • Geometric Series
  • Orthogonality of Sinusoids
  • Orthogonality of the DFT Sinusoids
  • Norm of the DFT Sinusoids
  • An Orthonormal Sinusoidal Set
  • The Discrete Fourier Transform (DFT)
  • Frequencies in the ''Cracks''
  • Normalized DFT
• The Length 2 DFT
• Matrix Formulation of the DFT
  • Matrices
  • Matrix Multiplication
  • The DFT Matrix
• Matlab Examples
  • Figure 7.2
  • Figure 7.3
  • DFT Matrix

<< Previous page  TOC  INDEX  Next page >>