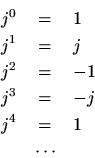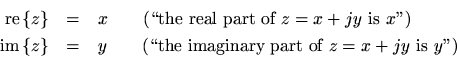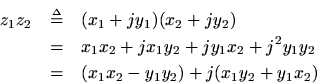Complex Numbers

GUIDE: Mathematics of the Discrete Fourier Transform (DFT) - Julius O. Smith III. Complex Numbers

It appears that you are using AdBlocking software. The cost of running this website is covered by advertisements. If you like it please feel free to a small amount of money to secure the future of this website.
​

NOTE: THIS DOCUMENT IS OBSOLETE, PLEASE CHECK THE NEW VERSION: "Mathematics of the Discrete Fourier Transform (DFT), with Audio Applications --- Second Edition", by Julius O. Smith III, W3K Publishing, 2007, ISBN 978-0-9745607-4-8. - Copyright © 2017-09-28 by Julius O. Smith III - Center for Computer Research in Music and Acoustics (CCRMA), Stanford University

<< Previous page  TOC  INDEX  Next page >>

Complex Numbers

This section introduces various notation and terms associated with complex numbers. As discussed above, complex numbers are devised by introducing the square-root of $-1$ as a primitive new algebraic object among real numbers and manipulating it symbolically as if it were a real number itself:

\

Mathemeticians and physicists often use $i$ instead of $j$ as $\. The use of $j$ is common in engineering where $i$ is more often used for electrical current.

As mentioned above, for any negative number $c<0$, we have $\, where $\ denotes the absolute value of $c$. Thus, every square root of a negative number can be expressed as $j$ times the square root of a positive number.

By definition, we have

\


and so on. Thus, the sequence $x(n)\, $n=0,1,2,\ is a periodic sequence with period $4$, since $j^{n+4}=j^n j^4=j^n$. (We'll learn later that the sequence $j^n$ is a sampled complex sinusoid havingfrequency equal to one fourth the sampling rate.)

Every complex number $z$ can be written as

\

where $x$ and $y$ are real numbers. We call $x$ the real part and$y$ the imaginary part. We may also use the notation
\


Note that the real numbers are the subset of the complex numbers having a zero imaginary part ($y=0$).

The rule for complex multiplication follows directly from the definition of the imaginary unit $j$:

\


In some mathematics texts, complex numbers $z$ are defined as ordered pairs of real numbers $(x,y)$, and algebraic operations such as multiplication are defined more formally as operations on ordered pairs, e.g., $(x_1,y_1) \. However, such formality tends to obscure the underlying simplicity of complex numbers as a straightforward extension of real numbers to include $j=\.

It is important to realize that complex numbers can be treated algebraically just like real numbers. That is, they can be added, subtracted, multiplied, divided, etc., using exactly the same rules of algebra (since both real and complex numbers are mathematicalfields). It is often preferable to think of complex numbers as being the true and proper setting for algebraic operations, with real numbers being the limited subset for which $y=0$.

To explore further the magical world of complex variables, see any textbook such as [4,5].


Subsections

<< Previous page  TOC  INDEX  Next page >>

​
 
​
© 1998-2023 – Nicola Asuni - Tecnick.com - All rights reserved.
about - disclaimer - privacy