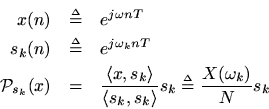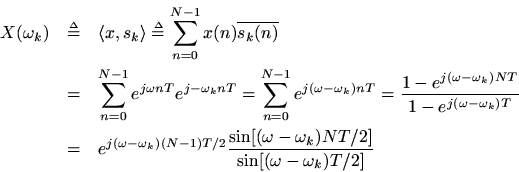Frequencies in the \

GUIDE: Mathematics of the Discrete Fourier Transform (DFT) - Julius O. Smith III. Frequencies in the \

It appears that you are using AdBlocking software. The cost of running this website is covered by advertisements. If you like it please feel free to a small amount of money to secure the future of this website.
​

NOTE: THIS DOCUMENT IS OBSOLETE, PLEASE CHECK THE NEW VERSION: "Mathematics of the Discrete Fourier Transform (DFT), with Audio Applications --- Second Edition", by Julius O. Smith III, W3K Publishing, 2007, ISBN 978-0-9745607-4-8. - Copyright © 2017-09-28 by Julius O. Smith III - Center for Computer Research in Music and Acoustics (CCRMA), Stanford University

<< Previous page  TOC  INDEX  Next page >>

Frequencies in the ''Cracks''

The DFT is defined only for frequencies $\. If we are analyzing one or more periods of an exactly periodic signal, where the period is exactly $N$ samples (or some integer divisor of $N$), then these really are the only frequencies present in the signal, and the spectrum is actually zero everywhere but at $\. However, we use the DFT to analyze arbitrary signals from nature. What happens when afrequency $\ is present in a signal $x$ that is not one of the DFT-sinusoid freqencies $\?

To find out, let's project a length $N$ segment of a sinusoid at an arbitrary freqency $\ onto the $k$th DFT sinusoid:

\


The coefficient of projection is proportional to
\


using the closed-form expression for a geometric series sum. As previously shown, the sum is $N$ at $\ and zero at $\, for$l\. However, the sum is nonzero at all other frequencies.

Since we are only looking at $N$ samples, any sinusoidal segment can be projected onto the $N$ DFT sinusoids and be reconstructed exactly by a linear combination of them. Another way to say this is that the DFT sinusoids form a basis for ${\, so that any length $N$ signal whatsoever can be expressed as linear combination of them. Therefore, when analyzing segments of recorded signals, we must interpret what we see accordingly.

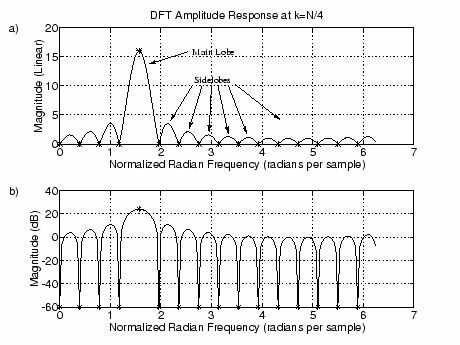
The typical way to think about this in practice is to consider the DFT operation as a digital filter.7.1 The frequency response of this filter is what we just computed,7.2 and its magnitude is

\

(shown in Fig. 7.3a for $k=N/4$). At all other integer values of$k$, the response is the same but shifted (circularly) left or right so that the peak is centered on $\. The secondary peaks away from$\ are called sidelobes of the DFT response, while the main peak may be called the main lobe of the response. Since we are normally most interested in spectra from an audio perspective, the same plot is repeated using a decibel vertical scale in Fig. 7.3b (clipped at $-60$ dB). We see that the sidelobes are really quite high from an audio perspective. Sinusoids with frequencies near $\, for example, are only attenuated approximately $13$ dB in the DFT output $X(\.
Figure 7.3:Frequency response magnitude of a single DFT output sample.
\

We see that $X(\ is sensitive to all frequencies between dc and the sampling rate except the other DFT-sinusoid frequencies$\ for $l\. This is sometimes called spectral leakageor cross-talk in the spectrum analysis. Again, there is no error when the signal being analyzed is truly periodic and we can choose$N$ to be exactly a period, or some multiple of a period. Normally, however, this cannot be easily arranged, and spectral leakage can really become a problem.

Note that spectral leakage is not reduced by increasing $N$. It can be thought of as being caused by abruptly truncating a sinusoid at the beginning and/or end of the $N$-sample time window. Only the DFT sinusoids are not cut off at the window boundaries. All other frequencies will suffer some truncation distortion, and the spectral content of the abrupt cut-off or turn-on transient can be viewed as the source of the sidelobes. Remember that, as far as the DFT is concerned, the input signal $x(n)$ is the same as its periodic extension. If we repeat $N$ samples of a sinusoid at frequency $\, there will be a ''glitch'' every $N$ samples since the signal is not periodic in $N$ samples. This glitch can be considered a source of new energy over the entire spectrum.

To reduce spectral leakage (cross-talk from far-away frequencies), we typically use a window function, such as a ''raised cosine'' window, to taper the data record gracefully to zero at both endpoints of the window. As a result of the smooth tapering, the main lobe widens and the sidelobes decrease in the DFT response. Using no window is better viewed as using a rectangular window of length $N$, unless the signal is exactly periodic in $N$ samples. These topics are considered further in Music 420 and in the ''Examples using the DFT'' chapter.

Since the $k$th spectral sample $X(\ is properly regarded as primarily a measure of spectral amplitude over the range$k-1/2$ to $k+1/2$, this range is sometimes called a frequency bin (as in a ''storage bin'' for spectral energy). The frequency index $k$ is called the bin number, and $\can be regarded as the total energy in the $k$th bin (see Parseval's Theorem in the ''Fourier Theorems'' chapter). Similar remarks apply to samples of any continuous bandlimited function; however, the term ''bin'' is only used in the frequency domain, even though it could be assigned exactly the same meaning mathematically in the time domain.

<< Previous page  TOC  INDEX  Next page >>

​
 
​
© 1998-2023 – Nicola Asuni - Tecnick.com - All rights reserved.
about - disclaimer - privacy