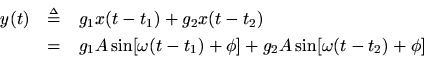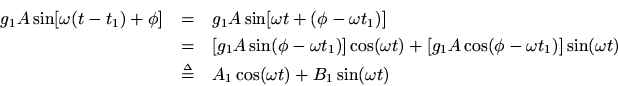NOTE: THIS DOCUMENT IS OBSOLETE, PLEASE CHECK THE NEW VERSION: "Mathematics of the Discrete Fourier Transform (DFT), with Audio Applications --- Second Edition", by Julius O. Smith III, W3K Publishing, 2007, ISBN 978-0-9745607-4-8. - Copyright © 2017-09-28 by Julius O. Smith III - Center for Computer Research in Music and Acoustics (CCRMA), Stanford University
<< Previous page TOC INDEX Next page >>
Sinusoids at the Same Frequency
An important property of sinusoids at a particular frequency is that they are closed with respect to addition. In other words, if you take a sinsusoid, make many copies of it, scale them all by different gains, delay them all by different amounts, and add them up, you always get a sinusoid at the same original frequency. This is a nontrivial property. It obviously holds for any constant signal
(which we may regard as a sinusoid at frequency
), but it is not obvious for
(see Fig. 5.2 and think about the sum of the two waveforms shown being precisely a sinusoid).
Since every linear, time-invariant (LTI5.1) system (filter) operates by copying, scaling, delaying, and summing its input signal(s) to create its output signal(s), it follows that when a sinusoid at a particular frequency is input to an LTI system, a sinusoid at that same frequency always appears at the output. Only the amplitude and phase can be changed by the system. We say that sinusoids are eigenfunctionsof LTI systems. Conversely, if the system is nonlinear or time-varying, new frequencies are created at the system output.
To prove the important invariance property of sinusoids, we may simply express all scaled and delayed sinusoids in the ''mix'' in terms of their in-phase and quadrature components and then add them up. For example, consider the case of two sinusoids arbitrarily scaled by gains
and arbitrarily delayed by time-delays
:
Focusing on the first term, we have
We similarly compute
and add to obtain
This result, consisting of one in-phase and one quadrature signal component, can now be converted to a single sinusoid at some amplitude and phase (and frequency), as discussed above.