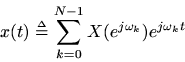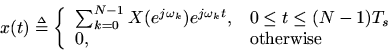Method 1: Additive Synthesis

NOTE: THIS DOCUMENT IS OBSOLETE, PLEASE CHECK THE NEW VERSION: "Mathematics of the Discrete Fourier Transform (DFT), with Audio Applications --- Second Edition", by Julius O. Smith III, W3K Publishing, 2007, ISBN 978-0-9745607-4-8. - Copyright © 2017-09-28 by Julius O. Smith III - Center for Computer Research in Music and Acoustics (CCRMA), Stanford University

<< Previous page  TOC  INDEX  Next page >>

Method 1: Additive Synthesis

One reasonable definition for can be based on the DFT of :

Since gives the magnitude and phase of the sinusoidal component at frequency , we simply construct as the sum of its constituent sinusoids, using continuous-time versions of the sinusoids:

This method is based on the fact that we know how to reconstruct sampled complex sinusoids exactly, since we have a ''closed form'' formulas for them. This method makes perfectly fine sense, but note that this definition of is periodic with period seconds. This happens because each of the sinusoids repeats after seconds. This is known as the periodic extensionproperty of the DFT, and it results from the fact that we had only samples to begin with, so some assumption must be made outside that interval. We see that the ''automatic'' assumption built into the math is periodic extension. However, in practice, it is far more common to want to assume zeros outside the range of samples:

Note that the nonzero time interval can be chosen as any length interval. Often the best choice is , which allows for both positive and negative times. (''Zero-phase filtering'' must be implemented using this convention, for example.)

''Chopping'' the sum of the ''DFT sinusoids'' in this way to zero outside an -sample range works fine if the original signal samples starts out and finishes with zeros. Otherwise, however, the truncation will cause errors at the edges, as can be understood from Fig. A.1.

<< Previous page  TOC  INDEX  Next page >>