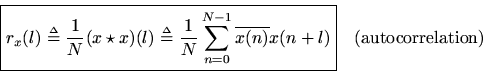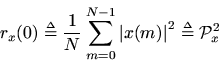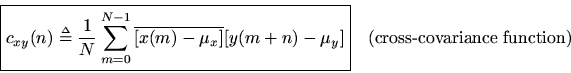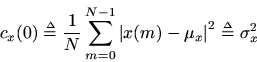Autocorrelation

NOTE: THIS DOCUMENT IS OBSOLETE, PLEASE CHECK THE NEW VERSION: "Mathematics of the Discrete Fourier Transform (DFT), with Audio Applications --- Second Edition", by Julius O. Smith III, W3K Publishing, 2007, ISBN 978-0-9745607-4-8. - Copyright © 2017-09-28 by Julius O. Smith III - Center for Computer Research in Music and Acoustics (CCRMA), Stanford University

<< Previous page  TOC  INDEX  Next page >>

Autocorrelation

The cross-correlation of a signal with itself gives the autocorrelation function

The autocorrelation function is Hermitian:

When is real, its autocorrelation is symmetric. More specifically, it is real and even.

As in the case of cross-correlation, we can form a true sample autocorrelation of sampled signals via

The DFT of the autocorrelation function is called the power spectral density (PSD), or ''power spectrum,'' and is often denoted

The true PSD of a ''stationary stochastic process'' is the Fourier transform of the true autocorrelation function, and therefore the definition above provides only a sample estimate of the PSD.

As in the case of the cross-spectrum, we may use the periodogram method for computing the power spectrum estimate. That is, we may estimate the power spectrum as the average of the DFTs of many sample autocorrelations which are computed block by block in a long signal, rather than taking one DFT of a single autocorrelation estimate based on all the data we have. By the Correlation Theorem, this is the same as averaging squared-magnitude DFTs of the signal blocks themselves. Let denote the th block of the signal , and let denote the number of blocks. Then the PSD estimate is given by

However, note that which is circularcorrelation. To avoid this, we use zero padding in the time domain, i.e., we replace above by . However, note that although the ''wrap-around problem'' is fixed, the estimator is still biased. To repair this, we can use a triangular window (also called a ''Bartlett window'') to apply the weighting needed to remove the bias.

For real signals, the autocorrelation is real and even, and therefore the power spectral density is real and even for all real signals. The PSD can interpreted as a measure of the relative probability that the signal contains energy at frequency . Essentially, however, it is the long-term average energy density vs. frequency in the random process .

At lag zero, the autocorrelation function reduces to the average power (root mean square) which we defined earlier:

Replacing ''correlation'' with ''covariance'' in the above definitions gives the corresponding zero-mean versions. For example, the cross-covariance is defined as

We also have that equals the variance of the signal :

<< Previous page  TOC  INDEX  Next page >>