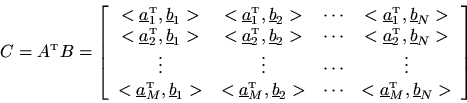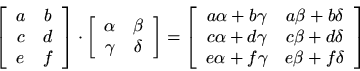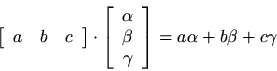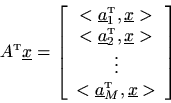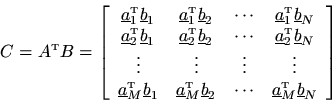Matrix Multiplication

01 Mar 1998

NOTE: THIS DOCUMENT IS OBSOLETE, PLEASE CHECK THE NEW VERSION: "Mathematics of the Discrete Fourier Transform (DFT), with Audio Applications --- Second Edition", by Julius O. Smith III, W3K Publishing, 2007, ISBN 978-0-9745607-4-8. - Copyright © 2017-09-28 by Julius O. Smith III - Center for Computer Research in Music and Acoustics (CCRMA), Stanford University

<< Previous page TOC INDEX Next page >>

Matrix Multiplication

Let $${A}^{\$ be a general $$M\$ matrix and let denote a general $$L\$ matrix. Denote the matrix product by $$C={A}^{\$ or $$C={A}^{\$ . Then matrix multiplication is carried out by computing the inner product of every row of $${A}^{\$ with every column of . Let theth row of $${A}^{\$ be denoted by $${\$ , $$i=1, 2,\$ , and theth column of by $$\$ , $$j=1,2,\$ . Then the matrix product $$C={A}^{\$ is defined as

This definition can be extended to complex matrices by using a definition of inner product which does not conjugate its second argument.^7.4
Examples:

An $$M\$ matrix can only be multiplied on the right by an $$L\$ matrix, where is any positive integer. An $$L\$ matrix can only be multiplied on the left by a $$M\$ matrix, where is any positive integer. Thus, the number of columns in the matrix on the left must equal the number of rows in the matrix on the right.

Matrix multiplication is non-commutative, in general. That is, normally $$AB\$ even when both products are defined (such as when the matrices are square.)

The transpose of a matrix product is the product of the transposes in reverse order:

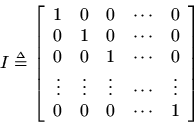
The identity matrix is denoted by and is defined as

Identity matrices are always square. The $$N\$ identity matrix , sometimes denoted as , satisfies $$A\$ for every $$M\$ matrix . Similarly, $$I_M\$ , for every $$M\$ matrix .
As a special case, a matrix $${A}^{\$ times a vector $$\$ produces a new vector $$\$ which consists of the inner product of every row of $${A}^{\$ with $$\$

A matrix $${A}^{\$ times a vector $$\$ defines a linear transformationof $$\$ . In fact, every linear function of a vector $$\$ can be expressed as a matrix multiply. In particular, every linear filtering operation can be expressed as a matrix multiply applied to the input signal. As a special case, every linear, time-invariant (LTI) filtering operation can be expressed as a matrix multiply in which the matrix is Toeplitz, i.e., $${A}^{\$ (constant along alldiagonals).
As a further special case, a row vector on the left may be multiplied by a column vector on the right to form a single inner product:

where the alternate transpose notation '' $$\$ '' is defined to include complex conjugation so that the above result holds also for complex vectors. Using this result, we may rewrite the general matrix multiply as

<< Previous page TOC INDEX Next page >>

GUIDE: Mathematics of the Discrete Fourier Transform (DFT) - Julius O. Smith III. Matrix Multiplication

Matrix Multiplication