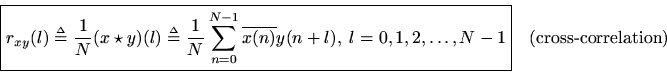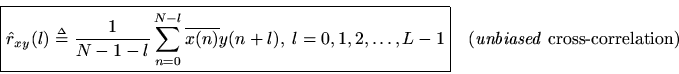NOTE: THIS DOCUMENT IS OBSOLETE, PLEASE CHECK THE NEW VERSION: "Mathematics of the Discrete Fourier Transform (DFT), with Audio Applications --- Second Edition", by Julius O. Smith III, W3K Publishing, 2007, ISBN 978-0-9745607-4-8. - Copyright © 2017-09-28 by Julius O. Smith III - Center for Computer Research in Music and Acoustics (CCRMA), Stanford University
<< Previous page TOC INDEX Next page >>
Cross-Correlation
Definition: The circular cross-correlation of two signalsand
in
may be defined by
(Note carefully above that '''' is an integer variable, not the constant
.) The term ''cross-correlation'' comes from statistics, and what we have defined here is more properly called the ''sample cross-correlation,'' i.e., it is an estimator of the true cross-correlation which is a statistical property of the signal itself. The estimator works by averaging lagged products
. The true statistical cross-correlation is the so-called expected value of the lagged products in random signals
and
, which may be denoted
. In principle, the expected value must be computed by averaging
over many realizations of the stochastic process
and
. That is, for each ''roll of the dice'' we obtain
and
for all time, and we can average
across all realizations to estimate the expected value of
. This is called an ''ensemble average'' across realizations of a stochastic process. If the signals are stationary (which primarily means their statistics are time-invariant), then we mayaverage across time to estimate the expected value. In other words, for stationary noise-like signals, time averages equal ensemble averages. The above definition of the sample cross-correlation is only valid for stationary stochastic processes.
The DFT of the cross-correlation is called the cross-spectral density, or ''cross-power spectrum,'' or even simply ''cross-spectrum.''
Normally in practice we are interested in estimating the true cross-correlation between two signals, not the circular cross-correlation which results naturally in a DFT setting. For this, we may define instead
where we chose(e.g.
) in order to have enough lagged products at the highest lag that a reasonably accurate average is obtained. The term ''unbiased'' refers to the fact that we are dividing the sum by
rather than
.
Note that instead of first estimating the cross-correlation between signals
and
and then taking the DFT to estimate the cross-spectral density, we may instead compute the sample cross-correlation for each block of a signal, take the DFT of each, and average the DFTs to form a final cross-spectrum estimate. This is called the periodogram method of spectral estimation.