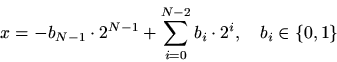NOTE: THIS DOCUMENT IS OBSOLETE, PLEASE CHECK THE NEW VERSION: "Mathematics of the Discrete Fourier Transform (DFT), with Audio Applications --- Second Edition", by Julius O. Smith III, W3K Publishing, 2007, ISBN 978-0-9745607-4-8. - Copyright © 2017-09-28 by Julius O. Smith III - Center for Computer Research in Music and Acoustics (CCRMA), Stanford University
<< Previous page TOC INDEX Next page >>
''Little Endian'' Formula for Two's-Complement, Integer Fixed-Point Numbers
The formula of the preceding section can be considered ''big endian'' because the bits are labeled ''left to right'' in the word as it is normally visualized. That is,
is the most significant bit instead of the least significant bit. The ''little endian'' convention numbers bits in order of their significance instead.
For the ''little-endian'' formula, we simply reverse the bits
in the previous formula:
The binary word is now written
The actual bits in the word are visualized the same in both big and little endian labelings. For example, in the three-bit case, a decimal 3 is still a binaryand a decimal -4 is still a binary
. Only the bit-symbol subscripts are different:
vs.
.
Note that this representation extends to any ''base'' (currently 2). For example, positive decimal integers can be expanded as
and an-digit integer is written as
. This type of ''positional notation'' was a major ''breakthrough invention'' in ancient times that greatly facilitated the handling of large numbers. (Have you ever tried working extensively with Roman numerals?)