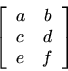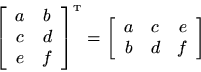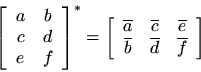Matrices

NOTE: THIS DOCUMENT IS OBSOLETE, PLEASE CHECK THE NEW VERSION: "Mathematics of the Discrete Fourier Transform (DFT), with Audio Applications --- Second Edition", by Julius O. Smith III, W3K Publishing, 2007, ISBN 978-0-9745607-4-8. - Copyright © 2017-09-28 by Julius O. Smith III - Center for Computer Research in Music and Acoustics (CCRMA), Stanford University

<< Previous page  TOC  INDEX  Next page >>

Matrices

A matrix is defined as a rectangular array of numbers, e.g.,

which is a (''two by two'') matrix. A general matrix may be , where is the number of rows, and is the number of columns. For example, the general matrix is

(Either square brackets or large parentheses may be used.) Theth element^7.3 of a matrix may be denoted by or . The rows and columns of matrices are normally numbered from instead of from; thus, and . When , the matrix is said to be square.

The transpose of a real matrix is denoted by and is defined by

Note that while is , its transpose is .

A complex matrix , is simply a matrix containing complex numbers. The transpose of a complex matrix is normally defined to includeconjugation. The conjugating transpose operation is called theHermitian transpose. To avoid confusion, in this tutorial, and the word ''transpose'' will always denote transpositionwithout conjugation, while conjugating transposition will be denoted by and be called the ''Hermitian transpose'' or the ''conjugate transpose.'' Thus,

Example: The transpose of the general matrix is

while the conjugate transpose of the general matrix is

A column-vector

is the special case of an matrix, and a row-vector

(as we have been using) is a matrix. In contexts where matrices are being used (only this section for this course), it is best to define all vectors as column vectors and to indicate row vectors using the transpose notation, as was done in the equation above.

<< Previous page  TOC  INDEX  Next page >>