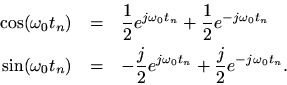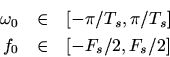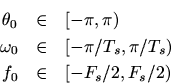NOTE: THIS DOCUMENT IS OBSOLETE, PLEASE CHECK THE NEW VERSION: "Mathematics of the Discrete Fourier Transform (DFT), with Audio Applications --- Second Edition", by Julius O. Smith III, W3K Publishing, 2007, ISBN 978-0-9745607-4-8. - Copyright © 2017-09-28 by Julius O. Smith III - Center for Computer Research in Music and Acoustics (CCRMA), Stanford University
<< Previous page TOC INDEX Next page >>
What frequencies are representable by a geometric sequence?
A natural question to investigate is what frequencies
are possible. The angular step of the point
along the unit circle in the complex plane is
. Since
, an angular step larger than
, say
is indistinguishable from the angular step
. Therefore, we must restrict the angular step
to a length
range in order to avoid ambiguity.
Recall that we need support for both positive and negative frequenciessince equal magnitudes of each must be summed to produce realsinusoids, as indicated by the identities
The lengthrange which is symmetric about zero is
which, since, corresponds to the frequency range
However, there is a problem with the point at: Both
and
correspond to the same point
in the
-plane. Technically, this can be viewed as aliasing of the frequency
on top of
, or vice versa. The practical impact is that it is not possible in general to reconstruct a sinusoid from its samples at this frequency. For an obvious example, consider the sinusoid at half the sampling-rate sampled on its zero-crossings:
. We cannot be expected to reconstruct a nonzero signal from a string of zeros! For the signal
, on the other hand, we sample the positive and negative peaks, and everything looks looks fine. In general, we either do not know the amplitude, or we do not know phase of a sinusoid sampled at exactly twice its frequency, and if we hit the zero crossings, we lose it altogether.
In view of the foregoing, we may define the valid range of ''digital frequencies'' to be
While you might have expected the open interval, we are free to give the point
either the largest positive or largest negative representable frequency. Here, we chose the largest negative frequency since it corresponds to the assignment of numbers in two's complement arithmetic, which is often used to implement phase registers in sinusoidal oscillators. Since there is no corresponding positive-frequency component, samples at
must be interpreted as samples of clockwise circular motion around the unit circle at two points. Such signals are any alternating sequence of the form
, where
can be be complex. The amplitude at
is then defined as
, and the phase is
.
We have seen that uniformly spaced samples can represent frequencies
only in the range
, where
denotes the sampling rate. Frequencies outside this range yield sampled sinusoids indistinguishable from frequencies inside the range.
Suppose we henceforth agree to sample at higher than twice the highest frequency in our continuous-time signal. This is normally ensured in practice by lowpass-filtering the input signal to remove all signal energy at
and above. Such a filter is called ananti-aliasing filter, and it is a standard first stage in anAnalog-to-Digital (A/D) Converter (ADC). Nowadays, ADCs are normally implemented within a single integrated circuit chip, such as a CODEC (for ''coder/decoder'') or ''multimedia chip''.