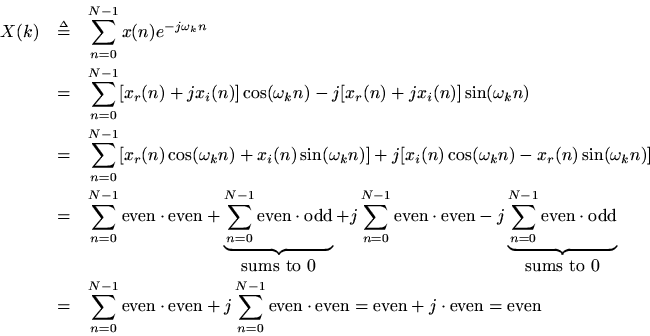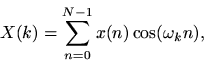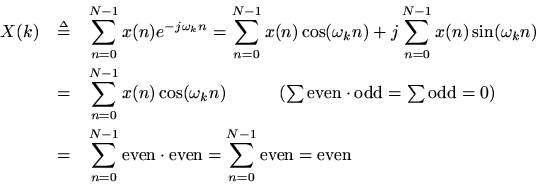NOTE: THIS DOCUMENT IS OBSOLETE, PLEASE CHECK THE NEW VERSION: "Mathematics of the Discrete Fourier Transform (DFT), with Audio Applications --- Second Edition", by Julius O. Smith III, W3K Publishing, 2007, ISBN 978-0-9745607-4-8. - Copyright © 2017-09-28 by Julius O. Smith III - Center for Computer Research in Music and Acoustics (CCRMA), Stanford University
<< Previous page TOC INDEX Next page >>
Symmetry
In the previous section, we found
when
is real. This fact is of high practical importance. It says that the spectrum of every real signal is Hermitian. Due to this symmetry, we may discard all negative-frequency spectral samples of a real signal and regenerate them later if needed from the positive-frequency samples. Also, spectral plots of real signals are normally displayed only for positive frequencies; e.g., spectra of sampled signals are normally plotted over the range
Hz to
Hz. On the other hand, the spectrum of a complex signal must be shown, in general, from
to
(or from
to
), since the positive and negative frequency components of a complex signal are independent.
Theorem: If,
is even and
is odd.
Proof: This follows immediately from the conjugate symmetry of
for real signals
.
Theorem: If,
is even and
is odd.
Proof: This follows immediately from the conjugate symmetry of
expressed in polar form
.
The conjugate symmetry of spectra of real signals is perhaps the most important symmetry theorem. However, there are a few more we can readily show.
Theorem: An even signal has an even transform:
Proof: Express
in terms of its real and imaginary parts by
. Note that for a complex signal
to be even, both its real and imaginary parts must be even. Then
Theorem: A real even signal has a real even transform:
Proof: This follows immediately from setting
in the preceding proof and seeing that the DFT of a real and even function reduces to a type of cosine transform8.5,
or we can show it directly:
Definition: A signal with a real spectrum (such as a real, even signal) is often called a zero phase signal. However, note that when the spectrum goes negative (which it can), the phase is really, not
. Nevertheless, it is common to call such signals ''zero phase, '' even though the phase switches between
and
at the zero-crossings of the spectrum. Such zero-crossings typically occur at low amplitude in practice, such as in the ''sidelobes'' of the DTFT of an FFT window.